ぜんぜんしりませんので一つずつ学んでいきます。
参考
5分でわかる!パーセプトロンの仕組みと実装方法(Python)
まずはシンプルな奴から見てみます。
単純パーセプトロン
言葉で言えば、2つの入力と、重みを
活性化関数で「0か1」に加工して出力するアルゴリズム?
あってます?
下図のような説明はよくありますね。
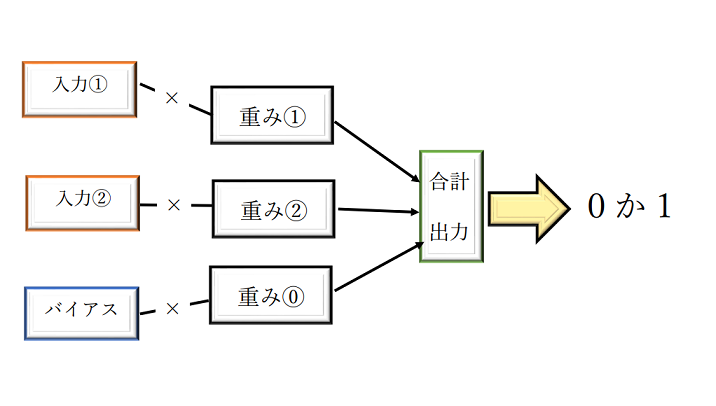
この入力を、「ノード」とか「ニューロン」と呼ぶらしい。
単純パーセプトロンの動き
(入力①×重み①) + (入力②×重み②) + (バイアス×重み⓪) = a
a ≦ 0 なら 0を出力
a > 0 なら 1を出力
となる。
この時のバイアスは、1を出力する度合いを調整するための値らしい。
そして、「重みとバイアスを調整するだけで出力を変えられる」ということがパーセプトロンの利点であり、ディープラーニングの根底を支える仕組み。
とあります。
ちょっとExcelで重みとバイアスを変更して表にしてみます。
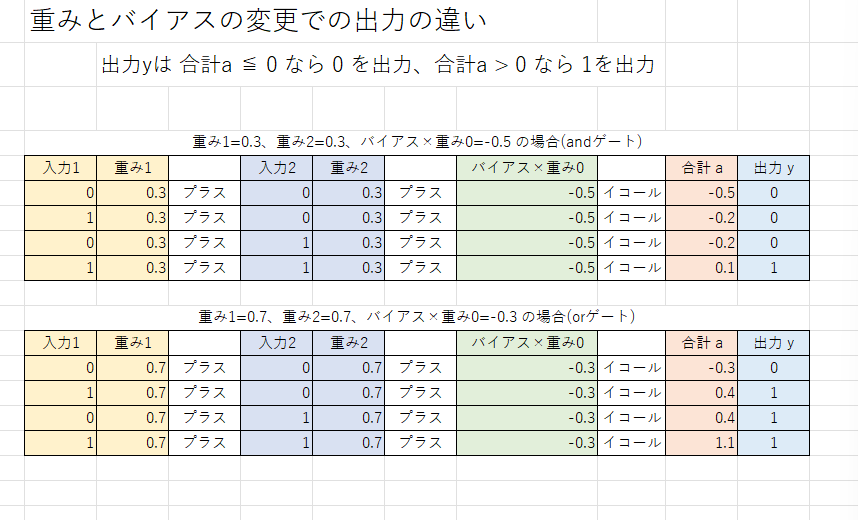
出力yの値が変わっているのがわかります。
ちなみに表上が ANDゲート、下が ORゲート だそうです。
まだ少しもやもやしています。
ANDゲート(論理和)とORゲート(論理積)
ANDゲート(論理積)
ANDゲートは、すべての入力が1であれば、1を出力し、それ以外は0を出力する。
| 入力1(x1) | 入力2(x2) | 出力(y) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
こういうことだそうです。
python標準の論理演算子andで実行してみます。
import numpy as np
x1 = np.array([0, 0, 1, 1]) # 入力は x とし、表のとおり数値を入力
x2 = np.array([0, 1, 0, 1])
for i in range(4):
y = x1[i] and x2[i] # python標準のand演算子で、4つの組み合わせを順に演算
print(y) # yは出力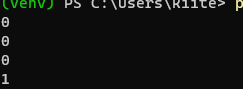
これをパーセプトロン関数というので書くこともできるらしい。
重みや、バイアスの数値はExcel表に従ってみた。
重み0.3 バイアス-0.5 に設定。
答えが同じなのはわかっていますが、一応。
import numpy as np
# パーセプトロン関数
def perceptron(x1, x2, w1, w2, bias, a):
f = w1 * x1 + w2 * x2 + bias
if f <= a: # fが、0より小さいか、等しいならば
y = 0 # 出力値は0
else:
y = 1 # それ以外は1
return y
x1 = np.array([0, 0, 1, 1])
x2 = np.array([0, 1, 0, 1])
w1 = 0.3 # 重みw1 を入力
w2 = 0.3 # 重みw2 を入力
bias = -0.5 # バイアス を入力
a = 0 # 基準値 aは、「0」
for i in range(4):
X1 = x1[i]
X2 = x2[i]
y = perceptron(X1, X2, w1, w2, bias, a)
print(y)
ORゲート(論理和)
ORゲートは、どちらかの入力が1であれば1を出力し、それ以外は0を出力。
| 入力1(x1) | 入力2(x2) | 出力(y) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
一応パーセプトロン関数でやってみた。
重み0.7 バイアス-0.3 に設定。
import numpy as np
# パーセプトロン関数
def perceptron(x1, x2, w1, w2, bias, a):
f = w1 * x1 + w2 * x2 + bias
if f <= a: # fが、0より小さいか、等しいならば
y = 0 # 出力値は0
else:
y = 1 # それ以外は1
return y
x1 = np.array([0, 0, 1, 1])
x2 = np.array([0, 1, 0, 1])
w1 = 0.7 # 重みw1 を入力
w2 = 0.7 # 重みw2 を入力
bias = -0.3 # バイアス を入力
a = 0 # 基準値 aは、「0」
for i in range(4):
X1 = x1[i]
X2 = x2[i]
y = perceptron(X1, X2, w1, w2, bias, a)
print(y)
ちゃんと結果が変わりました。
NANDゲート(ナンドゲート、否定論理積)
ANDゲートの反対
すべての入力が1であれば0を出力し、それ以外は1を出力する。
| 入力1(x1) | 入力2(x2) | 出力(y) |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
つまりバイアスと重みを変えることで、ゲートの種類を変えられる?
という解釈でよいのかな?
NANDゲートのコードを書くときは、
パラメーターの符号を、ANDゲートの反対にするようです。
import numpy as np
# パーセプトロン関数
def perceptron(x1, x2, w1, w2, bias, a):
f = w1 * x1 + w2 * x2 + bias
if f <= a: # fが、0より小さいか、等しいならば
y = 0 # 出力値は0
else:
y = 1 # それ以外は1
return y
x1 = np.array([0, 0, 1, 1])
x2 = np.array([0, 1, 0, 1])
w1 = -0.3 # 重みw1 ANDゲートの符号を反転
w2 = -0.3 # 重みw2 ANDゲートの符号を反転
bias = 0.5 # バイアス ANDゲートの符号を反転
a = 0 # 基準値 aは、「0」
for i in range(4):
X1 = x1[i]
X2 = x2[i]
y = perceptron(X1, X2, w1, w2, bias, a)
print(y)
おお!符号を反転したらできました!
XORゲートもあるんですね
でもこちらは、単純パーセプトロンでは実装できないそうです。
もう少し学習が進んだらにしましょう。