2023年5月 自分の学びのためのメモという位置づけです。
関数と聞いただけで
関数と聞いただけでもう面倒になります。
でも、関数はただの「変換器」との言葉に勇気づけられ、
ちょっとやってみよう。となります。
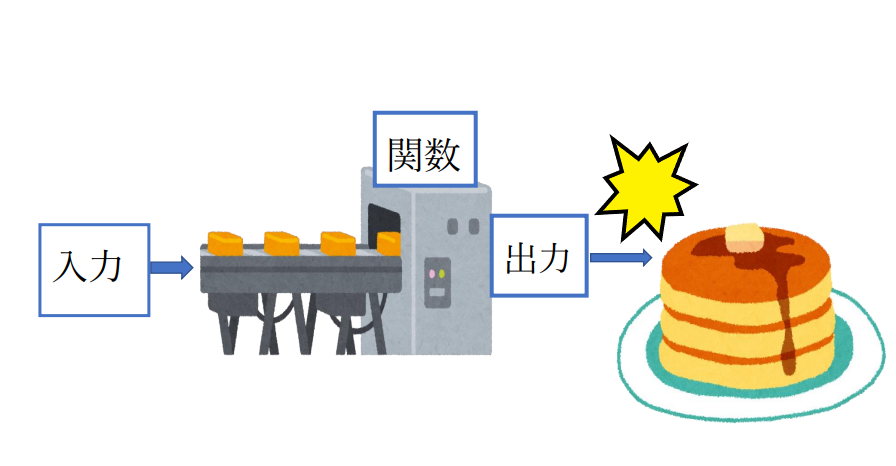
パーセプトロンの感じでいうとこんな図でしょうか
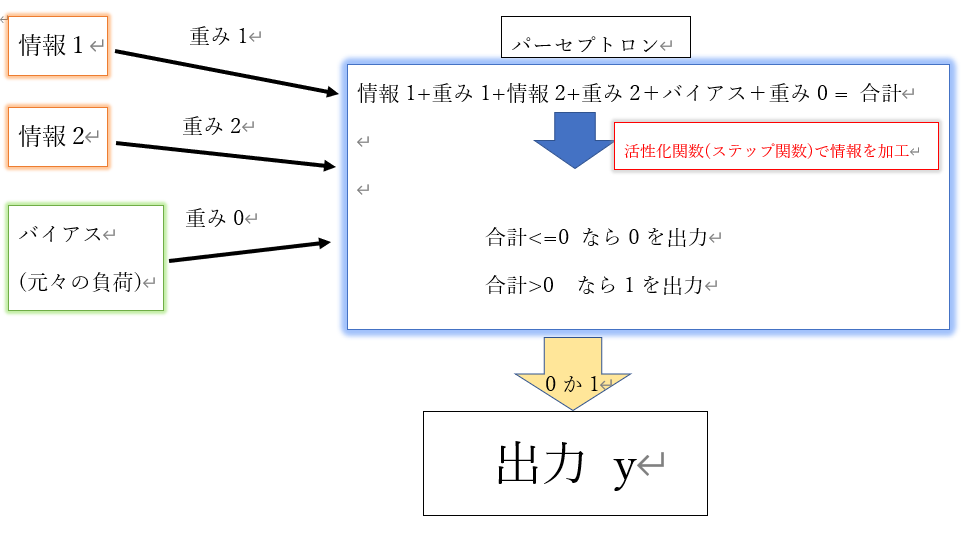
パーセプトロンでは「ステップ関数」というものを使っているんですね。
ステップ関数
ステップ関数は、入力が0を超えたら1を、それ以外は0を出力。
if x > 0:
return 1
else
return 0という感じになりますかね。
ステップ関数のグラフ
if x = 0 のような書き方をするときは、浮動小数点になっています。
浮動小数点は実数になっているので、(例 0.123456…….)
np.array([-0.1, 1.0, 2.0])のような使い方ができないようです。
※ ↑だと思う感じです。詳しい方教えてください!
それで、データーを変換(キャスト)する「astype」や
データーを初期化して指定する「dtype」を使用します。
y = x > 0
return y.astype(np.int64)というような感じです。
intは整数で、64はビット数です。
グラフを描画するには、matplotlibとnumpyを使用します。
import matplotlib.pylab as plt
import numpy as np
def step(x):
# dtypeで、データーを初期化してint(整数型)に指定する
return np.array(x > 0, dtype=np.int64)
x = np.arange(-5, 5.0, 0.1) # -5から5までの範囲を0.1刻みでnumpy配列にする
y = step(x)
# グラフの描画
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # y軸の範囲を指定
plt.show()実行するとこのようなグラフが出現します。
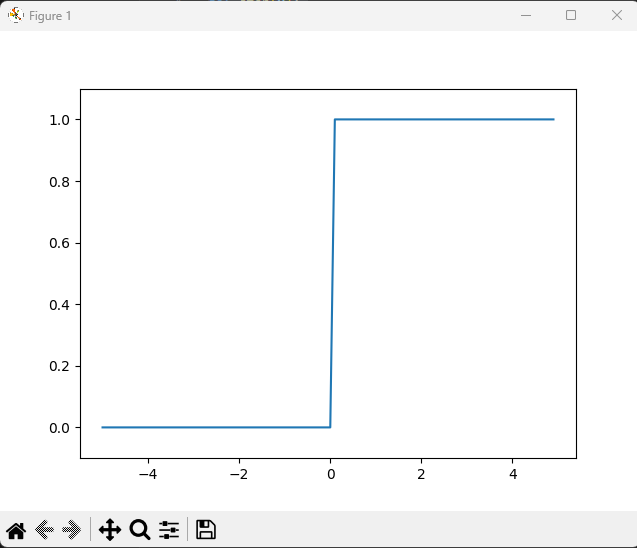
カクカクですね。
0を起点にして、1か0にスパッと分かれます。
竹を割ったような性格ですね。
シグモイド関数
$$f(x) = \frac{1}{1 + exp(-x)}$$
??もう理解する気にもなりません。
exp(-x)は、指数関数$$e^{-x}$$を表すそうです。
よくわかりませんが、eはネイピア数の2.7182…….の実数を表すそうです。
ここはそんなもんかで流します。
ただ、グラフにするときに、この式をそのまま入れる部分があります。
シグモイド関数のグラフ
細かいことは気にせずに、まずは実装して試してみましょう。
import matplotlib.pylab as plt
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x)) # シグモイド関数の式
x = np.arange(-5.0, 5.0, 0.1) # -5から5までの範囲を0.1刻みでnumpy配列にする
y = sigmoid(x)
# グラフ表示
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()こちらを実行すると、このようなブラフが表視されます。
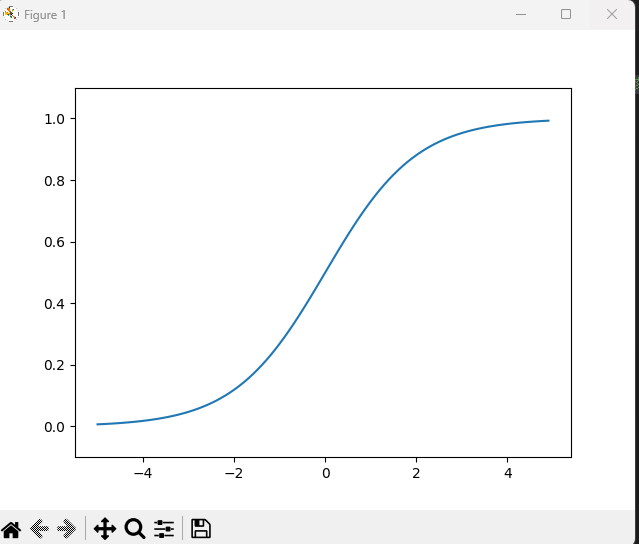
ステップ関数に比べてスムーズな曲線です。
この滑らかさが、ニューラルネットワークの学習において
大切なものだということです。
非線形関数
線形関数は一本の直線で描かれます。
ステップ関数も、シグモイド関数も曲線や階段線です。
これを「非線形関数」と呼ぶようです。
ニューラルネットワークには、非線形関数。
ここはとりあえずそれだけの理解にして、
次に行ってみます。
勾配消失問題
勾配消失問題とは?
誤差逆伝播法の際に、層が深いニューラルネットワークにおいて、
勾配がほぼ0になってしまい、学習がうまくいかない問題。
うんうん??
まず誤差逆伝播法をなるべく簡単に知りたい。。
ググるとこんな説明。
※ 誤差逆伝播法は、モデルに入力を与えて得られた出力とそれに対応する正解ラベルの誤差を求めたあと、その誤差を微分の連鎖律に基づいて出力側から入力側に逆伝播することで、各層のパラメータに関する勾配を計算する枠組みである。
本当はもっと奥深いもののようですが、なんとなく意味は分かりました。
これが何の問題につながるのでしょうか?
シグモイド関数、君が関係者だったのか・・
シグモイド関数の勾配(微分)の最大値は 0.25 である。
この最大値が 0.25 といった小さな値を持つ活性化関数は
勾配消失問題を引き起こしやすい!
じゃあ学習がうまくいかないではありませんか!
もう少し勾配消失問題を起こしにくい関数が必要なのですね。
ReLu関数
そこで用いられるのが、ReLu関数。
ReLu関数は、勾配の最大値が 1 。
シグモイド関数より勾配消失問題が緩和されるようです。
ReLU関数は、
入力が0を超えている場合 → 入力をそのまま出力
0以下の場合 → 0を出力する
シグモイド関数と同じ数値の条件で、グラフにしてみます。
最大値を取り出す max 関数を使用します。
import matplotlib.pylab as plt
import numpy as np
def relu(x):
return max(0, x) # maxは入力の最大値を取り出す
x = np.arange(-5.0, 5.0, 0.1) # -5から5までの範囲を0.1刻みでnumpy配列にする
y = [relu(a) for a in x]
# グラフ表示
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()次のような結果になりました。
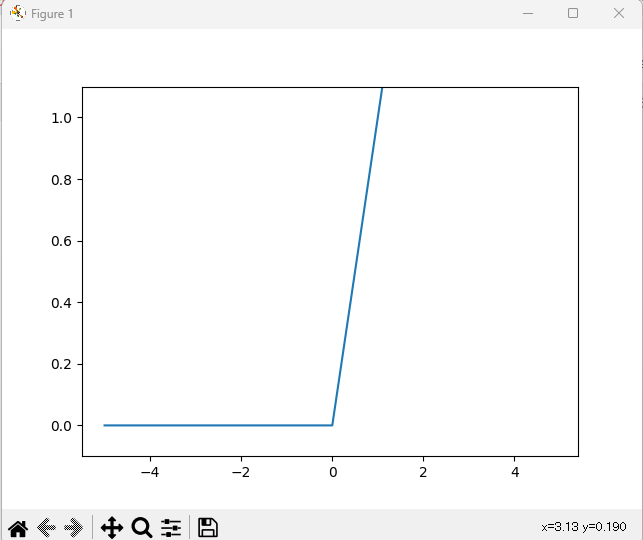
最近ではReLu関数を使用することが多いそうなのですが、
一つ疑問が残っています。
シグモイド関数のところで、
滑らかな曲線がニューラルネットワークの学習において重要とありました。
ReLu関数は「カクカク」?
とりあえずは、そういうものかと覚えておこうと思います。


